1.1 向量1.1.1 向量与坐标系将向量尾平移到坐标轴原点,就可以用向量头部坐标确定向量,记作v=(x,y,z),计算机就可以以三个浮点数来表示一个向量。 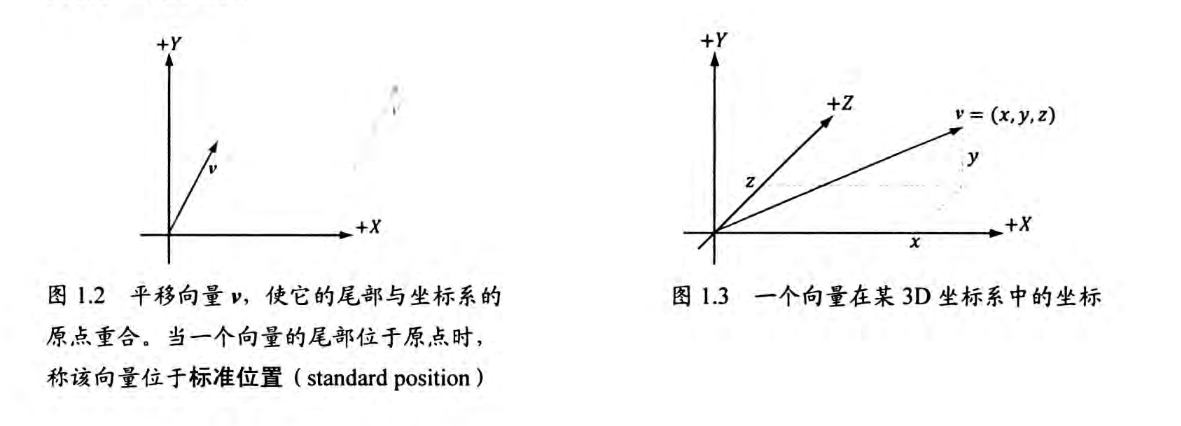 向量v在不同坐标系,的坐标不同,即同一向量在不同坐标系中有不同的坐标表示 这意味着:每当我们根据坐标来确定一个向量时,其对应坐标总是相对于某一参考系而言 我们需要记录向量在每一种坐标中的对应坐标,与需要知道如何将向量在不同空间下进行转换 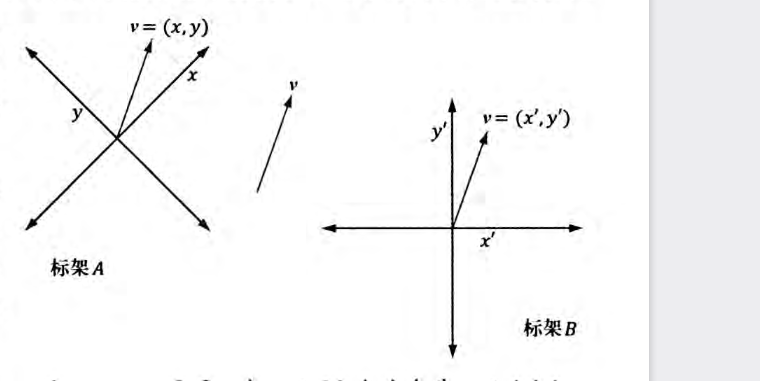 1.1.2 左手坐标系与右手坐标系Direct3D 采用左手坐标系。 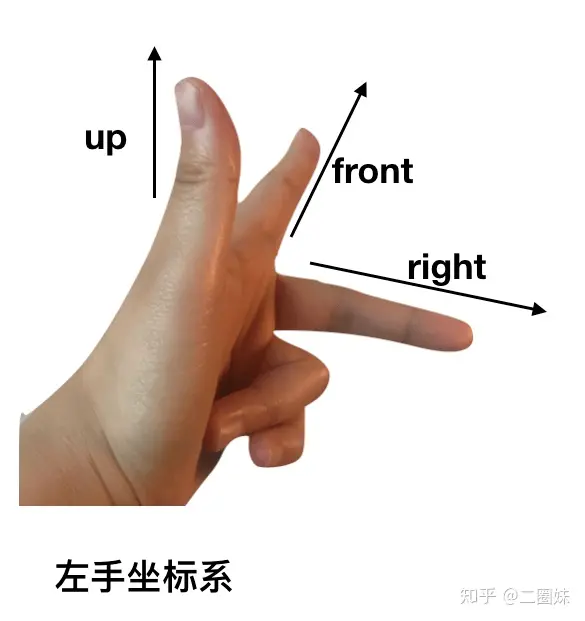 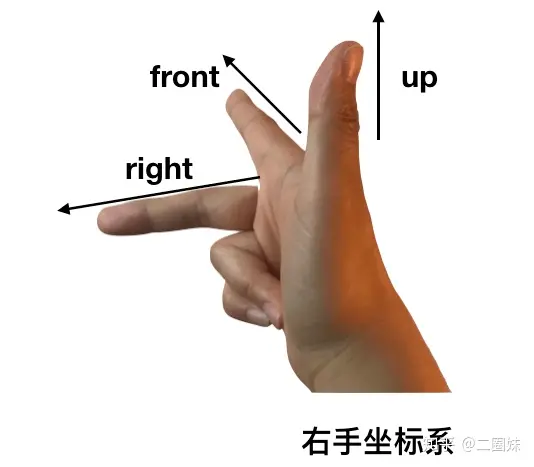 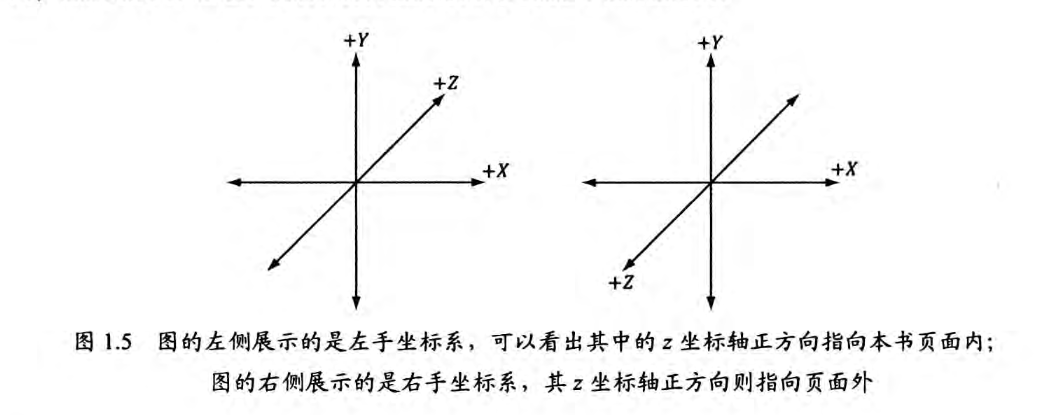 1.1.3 向量的基本运算分别有向量的相等,加法,减法,标量乘法运算,四种运算,如下图。  1.2 长度和单位向量使用毕达哥拉斯定理我们能得到向量模计算公式为: 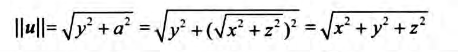 不关心长度,仅表示方向。我们希望使该向量长度为1.我们需要将向量进行归一化(将向量变为单位长度) 方法为将向量除以它的模:   1.3 点积点积的定义 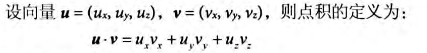 使用余弦定理计算两单位向量的cos值 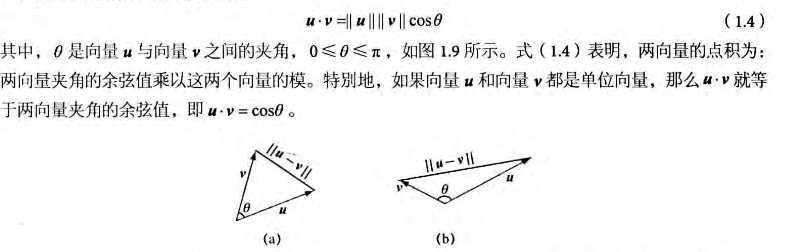 正交投影: 向量v在向量n方向上的正交投影  当n为单位向量时,可以推出 解释了 的几何意义 我们称p为向量v落在向量n上的正交投影,它被表示为:  将v看作一个力,可以认为p是力v在n方向上的奋力,同理向量 就是力v在n的正交方向上的分力。 可以观察到 ,也就是一个向量可以分解为两个互相正交的向量p和w 正交投影的一般公式: n不为单位向量时我们可以吧n替换为 得到一般性的投影公式 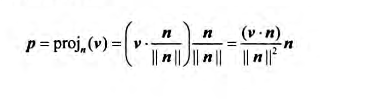 |
 |Archiver|手机版|小黑屋|软件开发编程门户
( 陇ICP备2024013992号-1|
|Archiver|手机版|小黑屋|软件开发编程门户
( 陇ICP备2024013992号-1|![]() 甘公网安备62090002000130号 )
甘公网安备62090002000130号 )
GMT+8, 2025-5-21 09:09 , Processed in 0.056496 second(s), 16 queries .
Powered by Discuz! X3.5
© 2001-2025 Discuz! Team.